Математика в механике грунтов
Федор Пинежанинов
Современный город - сложное явление. С точки зрения механики его можно рассматривать как техническую систему в которой взаимодействуют объекты различной природы, размещенные на бесконечном деформируемом полупространстве Земли.
Метод потенциалов связан с громоздкими вычислениями и не часто используется в
наше время, но для ряда задач на бесконечных областях удается осуществить
интегрирование аналитически и получить очень полезные формулы и оценки для
тестирования численных методов и для выбора конечных областей для моделирования
бесконечных. Кроме того подобные результаты позволяют оценить деформированное
состояние намного быстрее. Основа использования - интегральные представления
решений для уравнения Лапласа.
Будем рассматривать полупространство как способ моделирования реакций
неограниченной земли. Грунт является материалом, который сопротивляется сжатию и
практически не сопротивляется напряжению. Под действием гравитации он находится
в состоянии сжатия, поэтому практически даже если при решении получаются
растягивающие напряжения, то при сложении с гравитационными или бытовыми
напряжениями обычно получается что напряжения все равно остаются сжимающими, что
и позволяет говорить о упругом поведении. Основная характеристика грунтов
называется модуль деформаций. Это связано с тем, что реализуется множество
разнообразных пограничных контактных взаимодействий разрозненных однородных
частиц при этом возможно проскальзывание и перераспределение контактных пар.
Осредненная макрохарактеристика таких взаимодействий и называется модуль
деформаций, аналог модуля упругости в однородном сплошном теле. При нагружении
из - за перераспределения контактных пар часть поступающей при нагрузке энергии
расходуется на трение, что делает процесс необратимым, так как при снятии
нагрузки энергия на восстановление прежнего состояния не поступает и это
приводит к тому, что модули прямого и обратного нагружения (разгрузки )
значительно отличаются. В книге Тер - Мартиросяна дается примерное соотношение
между ними 5 ... 10. То есть модуль упругости при разгрузке значительно больше
модуля упругости прямого нагружения. Нормы рекомендуют в условиях
неопределенности принимать соотношение равное 5. Это важно при оценке влияния
котлованов на окружающую застройку. Так же важно учитывать при строительстве
нефтеналивных баков на слабых грунтах, когда в процессе испытаний происходит
нагрузка - разгрузка несколько раз и в итоге баки работают в режиме эксплуатации
на основаниях со значительно более высоким модулем деформаций, чем указан в
геологических данных. Такие же соображения можно отнести и к тяжелым
металлообрабатывающим станкам для энергетического оборудования со значительно
заглубленными фундаментами и высокими требованиями на их жесткость. Эти факты
автор наблюдал при сдаточных испытаниях построенных объектов. Многие современные
высотные здания имеют развитую подземную часть, что, по существу приводит к
разгрузке оснований и повторной нагрузке при возведении сооружения. То есть
модуль деформаций основания возрастает по сравнению с первоначальным.
Как известно из математической физики решение задачи Дирихле , когда заданы значения на поверхности полупространства для неизвестной функции уравнения Лапласа в трехмерном полупространстве дается формулой на основе потенциала двойного слоя
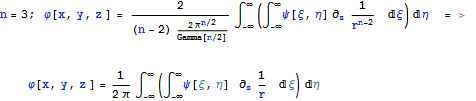
при этом будет соблюдаться
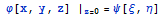 -
условие Дирихле и функция
-
условие Дирихле и функция
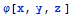 будет
гармоничной, то есть удовлетворяющей уравнению Лапласа,
при
будет
гармоничной, то есть удовлетворяющей уравнению Лапласа,
при 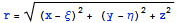 , где n - размерность
пространства.
, где n - размерность
пространства.
Это решение пригодно, если распределенное воздействие
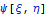 затухает на бесконечности с порядком
затухает на бесконечности с порядком
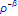
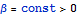 , Естественно, что
для измеримых воздействий на ограниченной области она справедлива всегда в
полупространстве. Здесь
, Естественно, что
для измеримых воздействий на ограниченной области она справедлива всегда в
полупространстве. Здесь 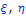 координаты
воздействия на поверхности полупространства
координаты
воздействия на поверхности полупространства
 =>
=>
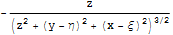
Таким образом, решение уравнения Лапласа для задачи Дирихле записывается
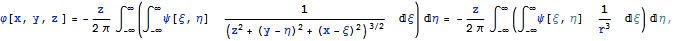
где ось z направлена внутрь полупространства.
Другая важная задача для уравнения Лапласа это задача Неймана, когда заданы значения производной по направлению нормали к границе полупространства на области границы полупространства. Ее решение дается формулой на основе потенциала простого слоя
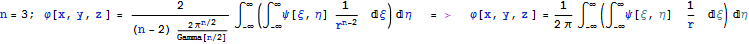
При этом будет соблюдаться условие Неймана
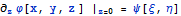 и функция
и функция
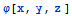 , будет гармоничной при
, будет гармоничной при
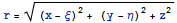
Это решение пригодно, если распределенное воздействие
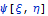 затухает на бесконечности с порядком
затухает на бесконечности с порядком
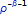 ,
,
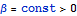
Естественно, что для воздействий ненулевых на ограниченной области она
справедлива всегда в полупространстве. Здесь
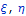 координаты воздействия на поверхности полупространства
координаты воздействия на поверхности полупространства
Задачи теории упругости для полупространства
В "Механике деформируемого твердого тела" Работнова показано, что для
упругого полупространства при отсутствии касательных нагрузок все перемещения,
как решение уравнения Навье - Коши теории упругости, выражаются через одну
гармоническую функцию, если равны нулю касательные напряжения
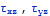 на границе полуплоскости.
Соответственно и деформации и напряжения как величины полученные от перемещений
в результате линейных преобразований в рамках линейной теории упругости.
Соответственно и деформации и напряжения как величины полученные от перемещений
в результате линейных преобразований в рамках линейной теории упругости.
на границе полуплоскости.
Соответственно и деформации и напряжения как величины полученные от перемещений
в результате линейных преобразований в рамках линейной теории упругости.
Соответственно и деформации и напряжения как величины полученные от перемещений
в результате линейных преобразований в рамках линейной теории упругости.
Из решения Папковича - Нейбера для однородного уравнения Навье - Коши для полупространства получается функциональное представление для перемещений через гармоническую функцию
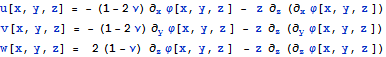
Используя линейные соотношения Коши для деформаций и закон Гука, можно
получить выражение напряжений через гармоническую функцию
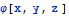
 =>
=>
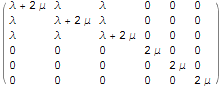 ,
, 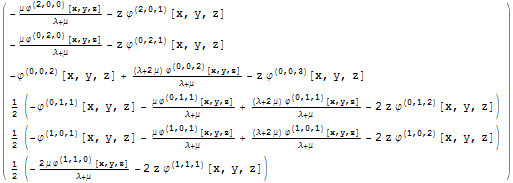
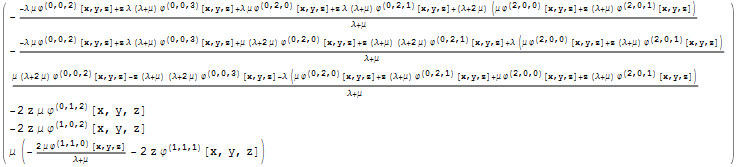
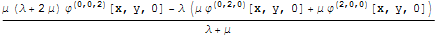
Рассмотрим напряжения на поверхности с учетом того, что
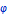 гармоническая и, следовательно, удовлетворяет
уравнению Лапласа
гармоническая и, следовательно, удовлетворяет
уравнению Лапласа
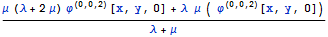
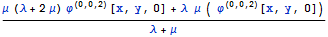 Упростим это выражение :
Упростим это выражение :
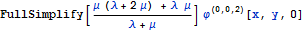 =>
=>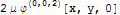 .
На поверхности полупространства при z = 0 получим
.
На поверхности полупространства при z = 0 получим
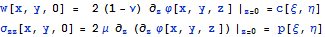 . Для сведения к задачам
Дирихле и Неймана из математической физики удобно ввести новую функцию
. Для сведения к задачам
Дирихле и Неймана из математической физики удобно ввести новую функцию
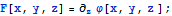 Тогда краевые условия можно переписать
Тогда краевые условия можно переписать
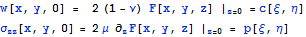 и следовательно решение задачи Дирихле можно
записать
и следовательно решение задачи Дирихле можно
записать
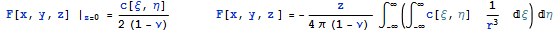 и решение задачи Неймана
и решение задачи Неймана
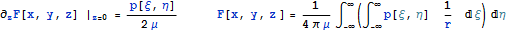
И далее, по описанным выше соотношениям для u, v, w, записать решение уравнения Навье - Коши для нагрузки, приложенной по нормали на границе полупространства , потом дифференцированием найти соотношения Коши для деформаций и по закону Гука найти напряжения.
Основная сложность при решении этих задач в вычислении кратных интегралов, которые далеко не всегда можно осуществить в замкнутом виде. Обычно нагрузки и перемещения заданы на ограниченных областях, а на остальных их можно считать заданными 0. Поэтому интегрирование достаточно проводить по области воздействия.
Далее рассмотрим практически важные задачи, решения которых можно получить в замкнутом виде.
Постоянное давление на прямоугольник. Задача Неймана
Результат решения этой задачи описан, например, у Коллинза.
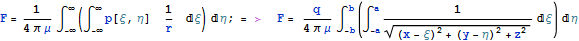 Ранее было из представления Папковича - Нейбера
Ранее было из представления Папковича - Нейбера
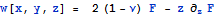

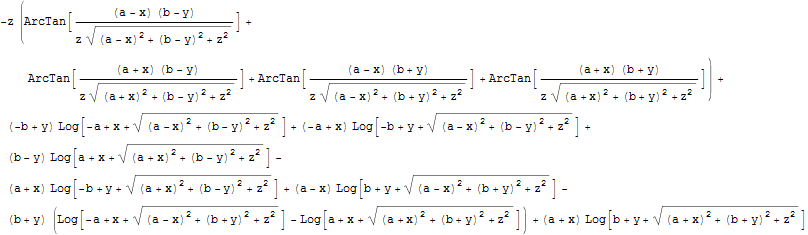




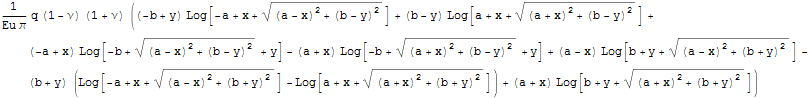
Приведем формулу из книги Джонсона и убедимся, что они аналогичны .
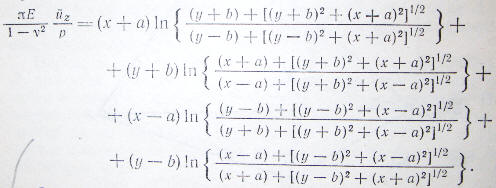
 =>
=>
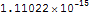
Вывод - при любых случайных числах на поверхности вертикальные перемещения
совпадают с точностью до машинной ошибки. Есть еще
способ проверить решение и принятое допущение "когда на граничной плоскости
равны нулю касательные напряжения" как отмечается в книге Работнова. Для этого
надо записать распределенное давление через главный вектор
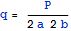 и устремить a и b к нулю.
В этом случае должны получить решение о сосредоточенной вертикальной силе
действующей на границу полупространства или решение задачи Буссинеска, взятое
например из книги Хана или Новацкого . Выражение для перемещений в общем
виде достаточно сложное, поэтому проверим два
случая, на поверхности и при начале координат по глубине
и устремить a и b к нулю.
В этом случае должны получить решение о сосредоточенной вертикальной силе
действующей на границу полупространства или решение задачи Буссинеска, взятое
например из книги Хана или Новацкого . Выражение для перемещений в общем
виде достаточно сложное, поэтому проверим два
случая, на поверхности и при начале координат по глубине
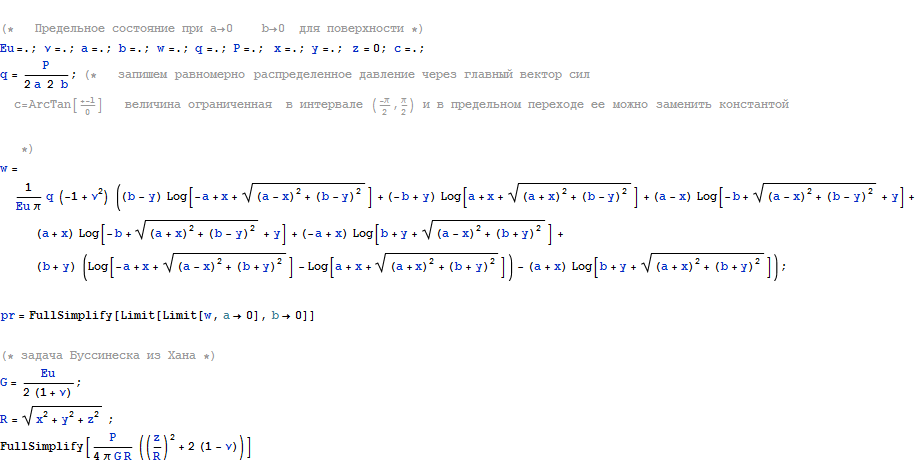
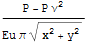 и
и
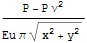

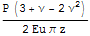
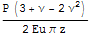
Вывод - в пределе при a->0 , b->0 полученное решение совпадает с решением Буссинеска для полупространства на поверхности и в глубину по z при x=y=0 и в силу гармоничности функций, как суперпозиции гармонических можно сделать вывод о совпадении на всем полупространстве.
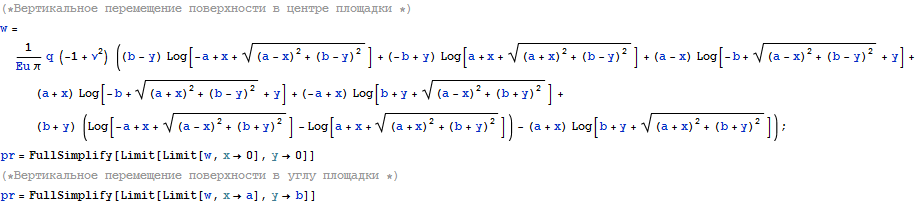
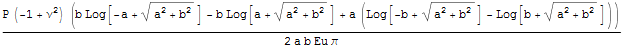

Можно упростить эти выражения введя отношение сторон в качестве новой переменной
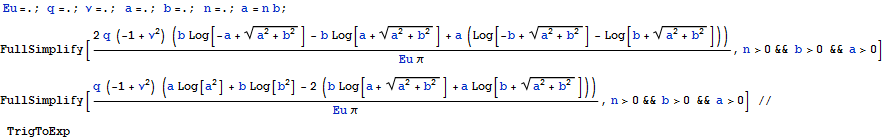
 и
и 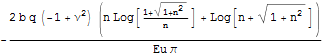
Убедимся, в равенстве 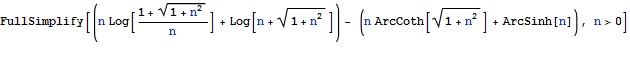 =>
0.
=>
0.
Следовательно, перемещение в центре площадки ровно в два раза больше перемещения в углу площадки и можем записать величину только для центра площадки.
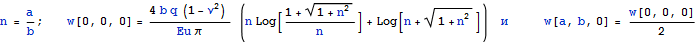
Такая запись в Help приложения к Ansys - CivilFem связывается с Steinbrenner 1936 г и используется для оценки осадок зданий.
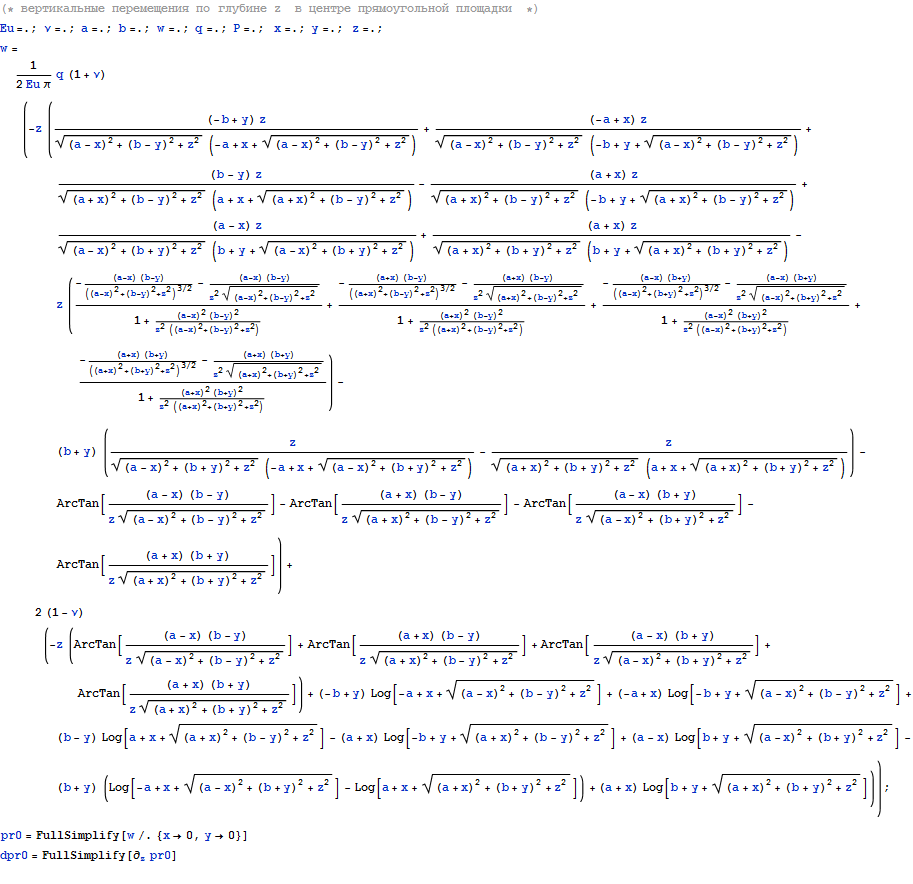
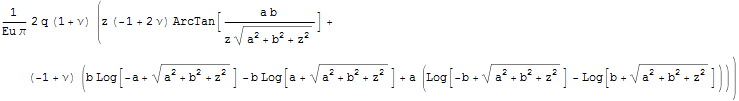
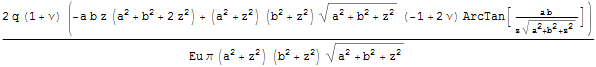

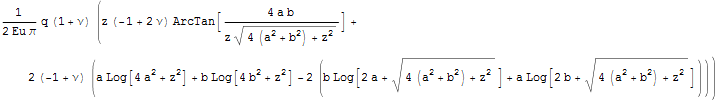
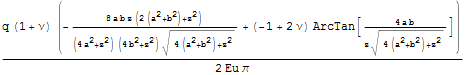
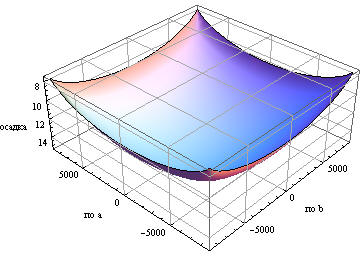
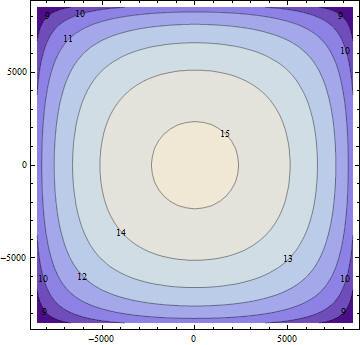
Чтобы увидеть характер поведения построим некоторые графики

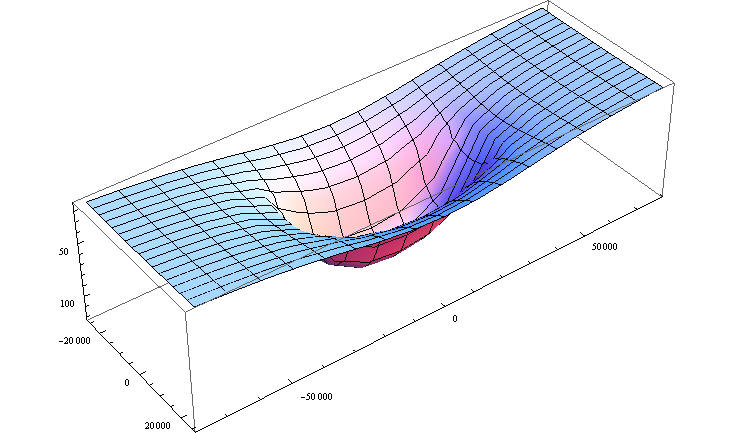
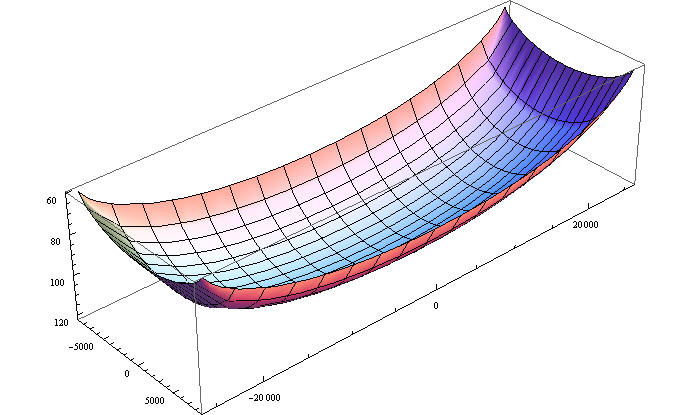
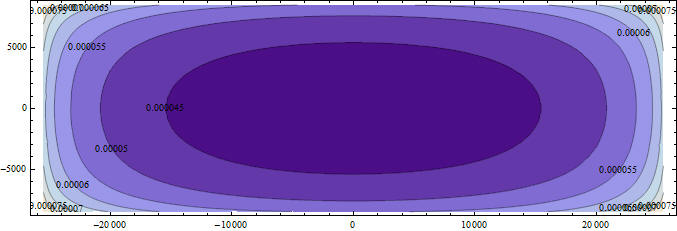
На последний рисунок можно смотреть как на распределенную жесткость основания при гибком здании, если учесть, что C u=F => C=F/u.

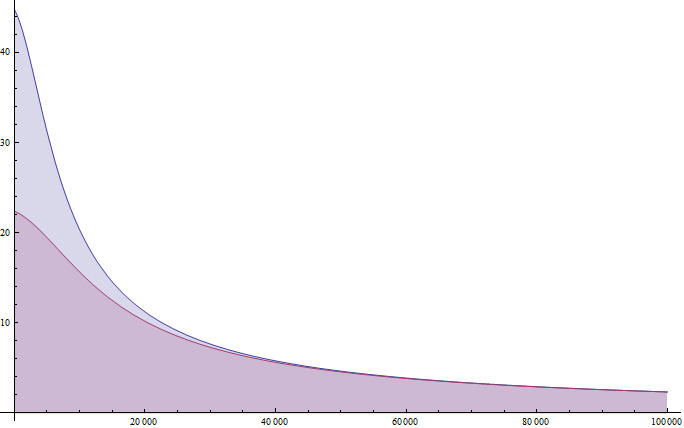
Деформации по вертикали
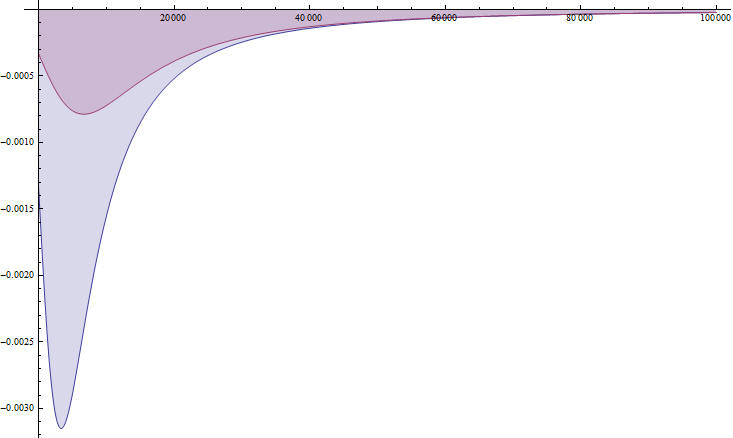
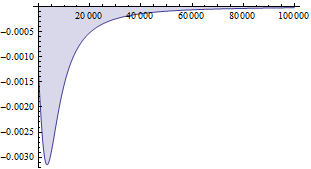
Для решения задач по влиянию зданий на окружающую застройку обычно
используется метод конечных элементов. Он эффективно решает задачи на
ограниченных областях и необходимо выбирать размеры окружающей земли, которую
надо моделировать и приведенная выше формула позволяет оценить погрешность
которая будет в численном решении.С другой стороны очевидно использование приема
известного как иерархическое уточнение на основе метода сечений . Рассматривая
аналитическое решение на бесконечном полупространстве как приближение, находим
перемещения на плоскостях разреза области которую собираемся моделировать и
используем эти перемещения в качестве краевых условий на перемещения в
моделируемой области. Профессиональные программы метода конечных элементов
обычно позволяют легко это реализовать. Этот же подход удобно использовать в
ситуациях, когда необходимо учитывать гравитационное сжатие грунта при оценке
влияния котлованов на окружающую застройку. Сначала
оцениваются перемещения поверхности земли без вносимого возмущения, затем эти
перемещения с обратным знаком используются в качестве краевых условий на
перемещения нижней границы моделируемой области грунта. Гравитационные
воздействия на грунт необходимо учитывать и при оценке коэффициентов запаса по
устойчивости грунта в котлованах при использовании теорий прочности типа
Кулона-Мора или Друкера-Прагера. В программе Ansys
несложно написать макрос на основе аналитического решения для автоматизации этих
технологий. Учитывая, что пластические эффекты
локализованы в области возмущения и учитывая принцип Сен-Венана возможна и
суперпозиция этих подходов на плоскостях границы конечной области, моделирующей
бесконечное полупростанство. В случае произвольной
границы для конечной области бесконечного полупростанства, моделируемого
конечной областью из конечных элементов, не сложно в цикле по узлам вычислить
перемещения в них по аналитической формуле, или определить жесткости для пружин
с одним закрепленным узлом размещенных в этих узлах используя соотношение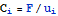 где F - главный вектор нагрузки, при котором надо решить задачу.
где F - главный вектор нагрузки, при котором надо решить задачу.
Если конечноэлементная программа имеет модуль оптимизации, как Ansys, то согласованные размеры окружающей земли удобно подобрать решая задачу оптимизации, где в качестве целевой функции выступает норма невязки между аналитическим решением и вертикальными перемещениями конечной области на модельной задаче. При этом в качестве переменных оптимизации можно использовать не только геометрические размеры, но и упругие постоянные, если интересует только адекватный отклик грунта.
В первом приближении можно прикладывать постоянное перемещение, или задавать точечные жесткости, определенное на достаточно заглубленной нижней границе. Это постоянное перемещение можно определить как среднее для уровня z определенного из аналитического решения. Есть еще вопрос о размерах зоны в горизонтальной плоскости. Из аналитического решения по смещениям поверхности можно определить замкнутую линию, которая имеет такие же смещениякак и средняя нижняя граница и прикладывать на них соответствующие условия. Или обеспечить на боковых поверхностях условия скольжения, которые, согласованно с ужесточением нижней плоскости вносимые в задачу однородными краевыми условиями, ослабят жесткость области для более точного приближения. В первом приближении можно использовать что-то вроде приведенного ниже кода:

Заданная глубина сжимаемой толщи мм = 200000
Максимальная осадка на этой глубине мм = 7.50576
Половина размера области для x мм = x->202475.
Половина размера области для y мм = y->204495.
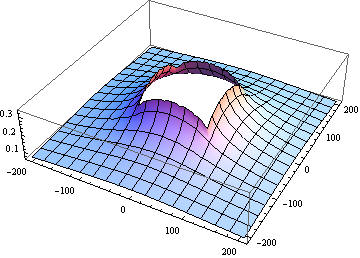
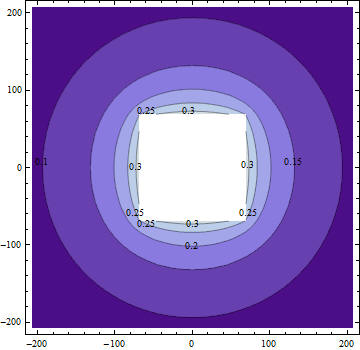
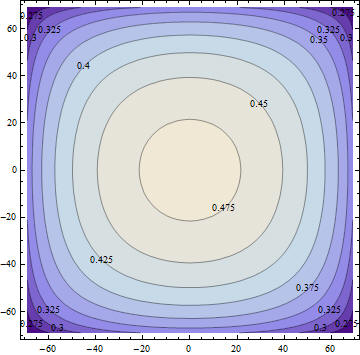
Подобные технологии полезны для анализа возмущений вносимых в старую застройку новыми сооружениями. Ниже пример подобных расчетов для строительства подземного сооружения методом сверху вниз в исторической части Санкт-Петербурга. Прогнозируемый подъем грунта из-за строительства котлована в мм.

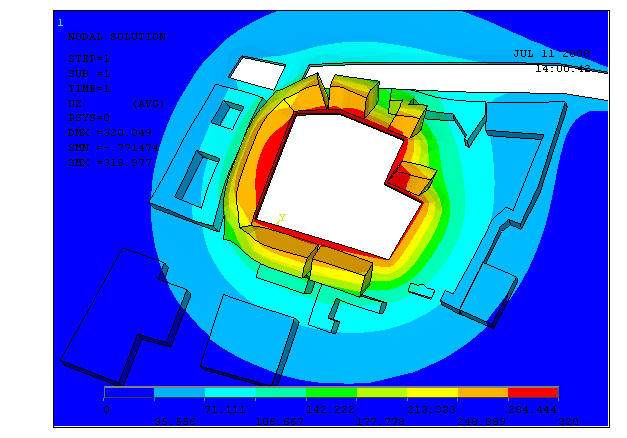
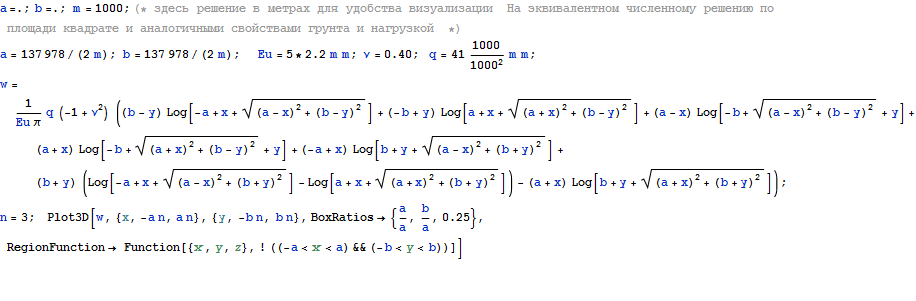

0.3
50.4124
{47.9294, 39.649}

Главный вектор нагрузки = -1.45656*10^6
Осадка в центре нагружаемой площадки = 15.2389
Осадка в углу нагружаемой площадки = 7.61944
Осадка посередине длинного ребра нагружаемой площадки = 10.4001
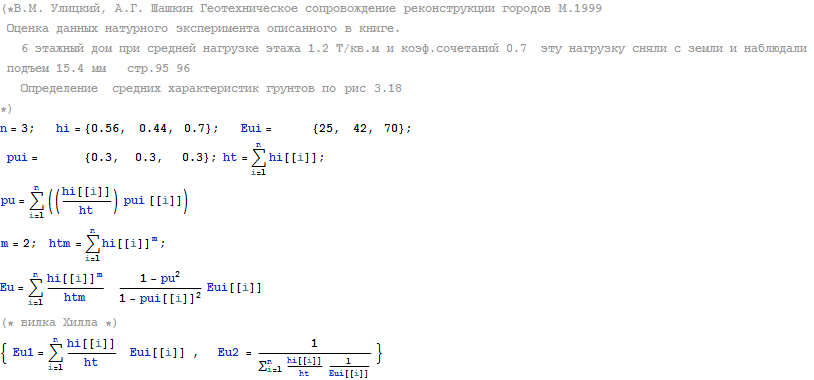
Вывод - упругое решение Лява, при модуле разгрузки равным 5 модулям прямого нагружения дает хорошее согласование с результатами натурного эксперимента, описанного в книге - Геотехническое сопровождение реконструкции городов, Улицкого и Шашкина, М.1999 Перенесем эти результаты по теории физического подобия на рассматриваемую область

Подъем натуры в мм = 462.181
Сравнив с ранее вычисленным по аналитическому решению, можно увидеть хорошее совпадение с данными натурного эксперимента.
Функции Грина
Для решения задачи Неймана можно использовать и другой подход
связанный с фундаментальными решениями задач теории упругости или единичными
точечными воздействиями на полупространство. Рассмотрим уравнение Навье - Коши
как дифференциальный оператор L и предположим существование обратного
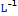 . Тогда решение уравнения L u = q
можно записать в виде
. Тогда решение уравнения L u = q
можно записать в виде 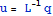 . Для
единичного точечного воздействия q есть дельта - функция Дирака. Как принято,
обозначим решение, связанное с единичным точечным воздействием и откликом на
него
. Для
единичного точечного воздействия q есть дельта - функция Дирака. Как принято,
обозначим решение, связанное с единичным точечным воздействием и откликом на
него 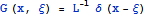 , это,
по существу, и есть функция Грина для
дифференциального уравнения. Физически разумные
воздействия обычно континуальны, поэтому, на функцию Грина можно смотреть как на
базис построенный на основе разложения по дельта-функциям и результат
воздействия распределения
, это,
по существу, и есть функция Грина для
дифференциального уравнения. Физически разумные
воздействия обычно континуальны, поэтому, на функцию Грина можно смотреть как на
базис построенный на основе разложения по дельта-функциям и результат
воздействия распределения 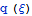 записать в континуальном виде :
записать в континуальном виде :
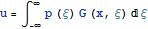 , здесь x и
, здесь x и
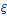 векторы в соответствующих
пространствах. При этом краевые условия соблюдаются автоматически, так как
учтены при построении функции Грина. Для задачи о воздействии вертикальной
распределенной нагрузки на часть поверхности полупространства в теории упругости
функцией Грина является решение Буссинеска для нормальной сосредоточенной силы
на поверхности полупространства при единичном воздействии поэтому можем сразу
записать решение для вертикальных осадок при действии равномерно распределенной
нагрузки на прямоугольную область поверхности
векторы в соответствующих
пространствах. При этом краевые условия соблюдаются автоматически, так как
учтены при построении функции Грина. Для задачи о воздействии вертикальной
распределенной нагрузки на часть поверхности полупространства в теории упругости
функцией Грина является решение Буссинеска для нормальной сосредоточенной силы
на поверхности полупространства при единичном воздействии поэтому можем сразу
записать решение для вертикальных осадок при действии равномерно распределенной
нагрузки на прямоугольную область поверхности

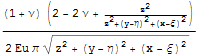

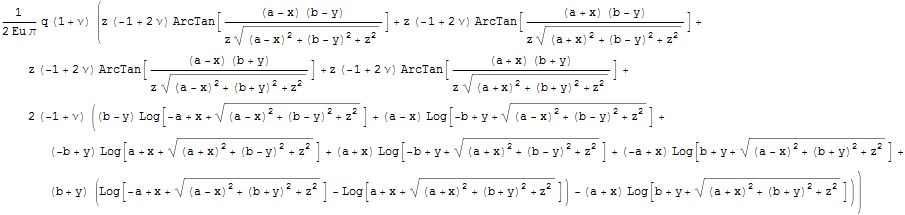
Посмотрим, что получается для поверхности, для этого как и ранее учтем ограниченность арктангенса тем, что введем z0 для z вне арктангенсов, обнулим, а потом и остальные z для исключения противоречий из - за деления на нуль в аргументах арктангенсов.
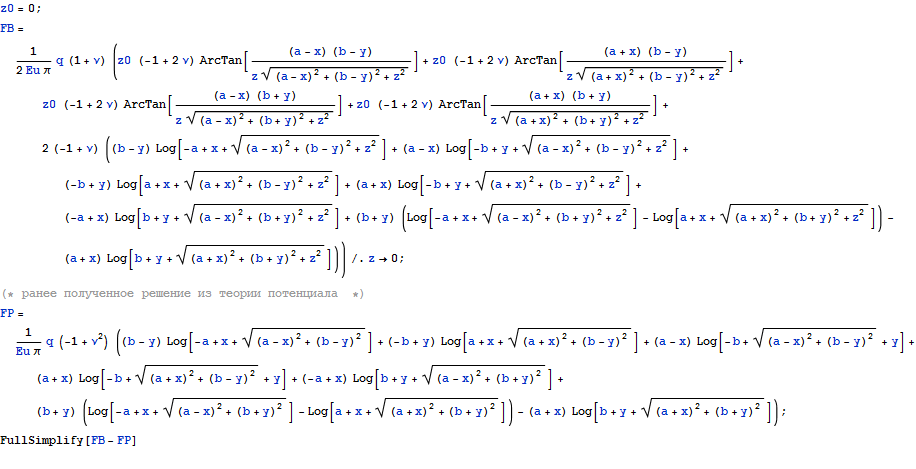
0
Видим, что решение, полученное на основе использования теории потенциала, совпадает с решением, полученным с использованием решения Буссинеска в качестве функции Грина для задачи Неймана уравнения Навье-Коши на поверхности.
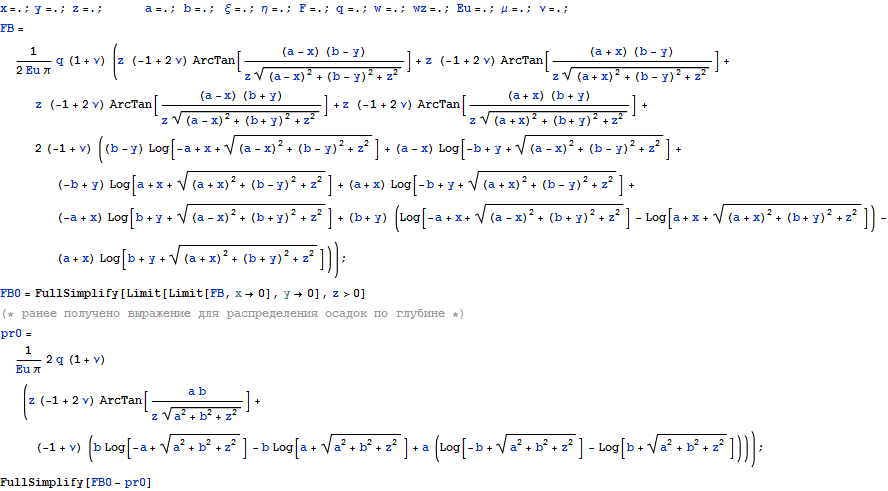
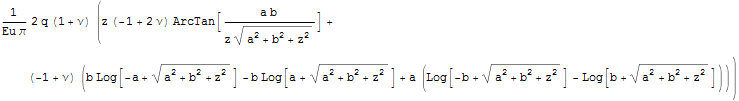
0
Этот результат говорит о том, что фундаментальное решение Буссинеска правильно описывает решение и в глубине полупространства.

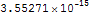
К сожалению ноутбук не справился с аналитическим упрощением, поэтому проверка общего случая проведена численно на псевдослучайных числах из физически разумного диапазона.Подход связанный с функциями Грина позволяет легко получать решения и для горизонтальных сил на поверхности полупространства, используя задачу Черрути в качестве функции Грина. Задача Миндлина о сосредоточенной силе внутри полупространства дает функцию Грина для решения задач о заглубленных фундаментах. Все эти задачи описаны у Хана и у Новацкого.
Постоянное перемещение прямоугольника. Задача Дирихле
Решение задачи Дирихле можно записать
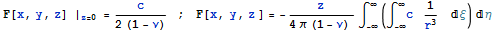
Как и в случае задачи Неймана интегрирование достаточно проводить по области с заданными ненулевыми граничными условиями
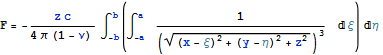

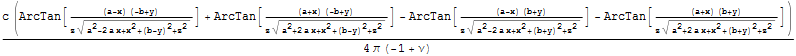
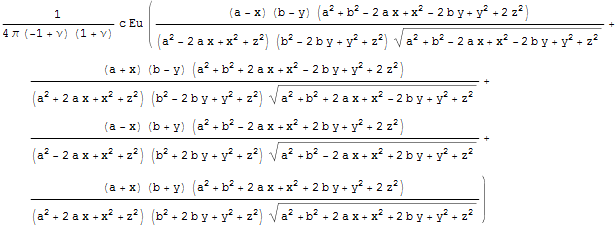
Упростим еще через фрагменты и запишем на поверхности при z = 0, вне области штампа напряжения нулевые.
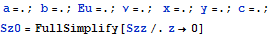
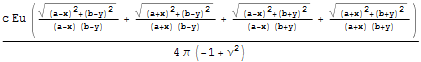
Это выражение задает распределение вертикальных напряжений при вдавливании прямоугольного штампа на единичную длину. Проинтегрируем по площади и отнормируем на полученную константу. Тогда в силу линейности задачи теории упругости можем трактовать как распределение давлений при единичном среднем давлении на площадку, а умножив на среднее по прямоугольной площадке давление получим формулу распределения реального давления. Исследуем нелинейную часть выражения
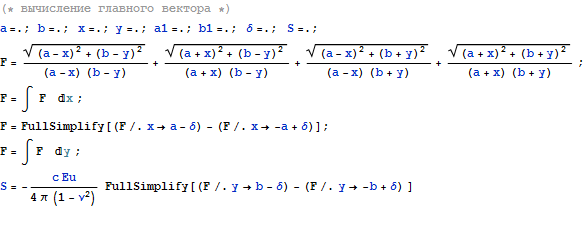
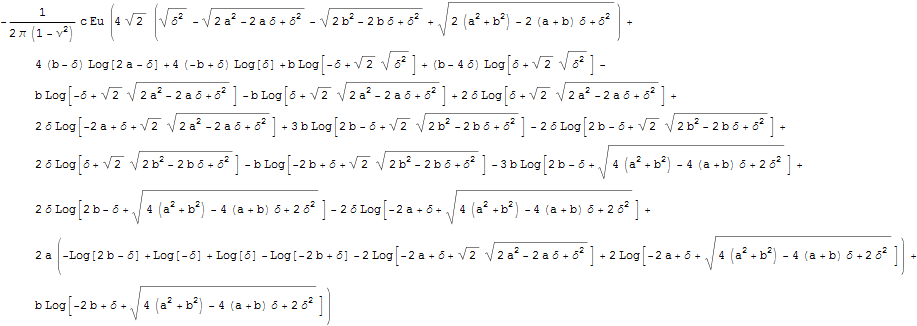
Взяв предел убедимся, что предел не сходится к конечному пределу.
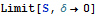 =>
=>
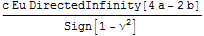
Для инженерных приложений это нереальная ситуация, так как бесконечных напряжений быть не может. Есть естественное ограничение, из - за предельного состояния материала. Поэтому есть две возможности для нормировки и приближения. Первая рассматривать распределение на открытом множестве, исключив границу с бесконечно - малой окрестностью, так как по замечанию Куранта, исследователь сам решает, что считать бесконечно малым, а что большим, но коль решил, то далее соотношения между величинами диктует математика. Это актуализация концепта бесконечно малой величины. С другой стороны, можно доопределить функцию распределения давления ограничением на рост, и по достижению того, что считается большим зафиксировать в виде константы, актуальной бесконечности. Это связано с тем, что абсолютно точное в рамках гармонических функций решение становится бесполезным и надо или сохранять гармоничность, на меньшей области, или допустить изломы. Но это только на поверхности, в глубине полупространства все остается гладким.

0.00205422
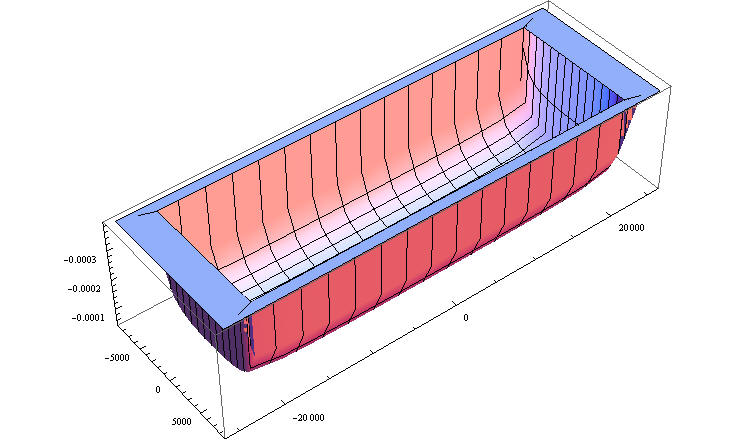
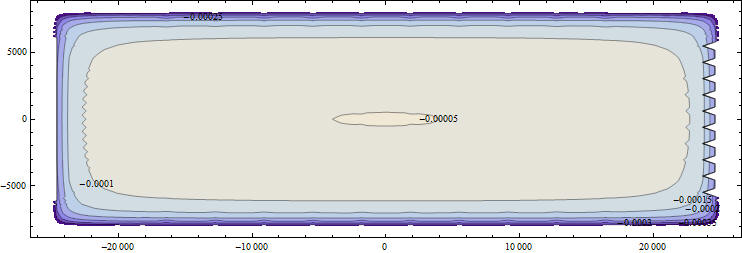
Интересный подход использования гладких функций для подобных задач связан с работами Александрова по ассимптотическим приближениям нагрузки к постоянной. Рассмотрим функцию F вида
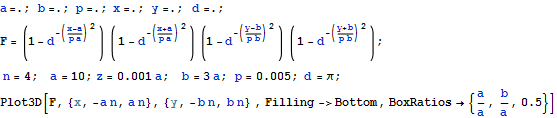
Из рисунка видно, что везде кроме окрестности границы функция равна единице и гладко сходит на 0 на границе. Здесь d,p параметры с помощью которых можно управлять граничной области. На границе эта функция имеет ноль более высокого порядка и поэтому если в знаменателе функции которую умножим на F , линейное приближение к нулю, то в результате получим 0 на границе. По существу это управляемое параметрами исключение границы из области интегрирования. Запишем распределение напряжений под жестким штампом с учетом этой функции.
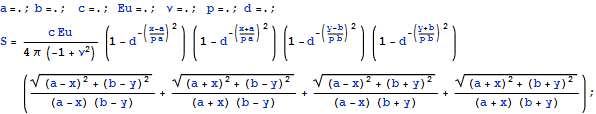

0.000915344
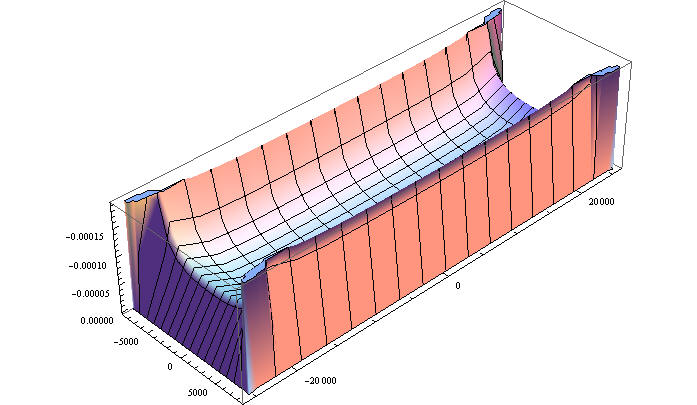
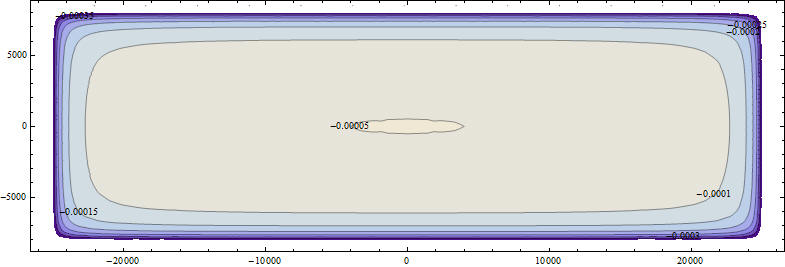

0.00062226
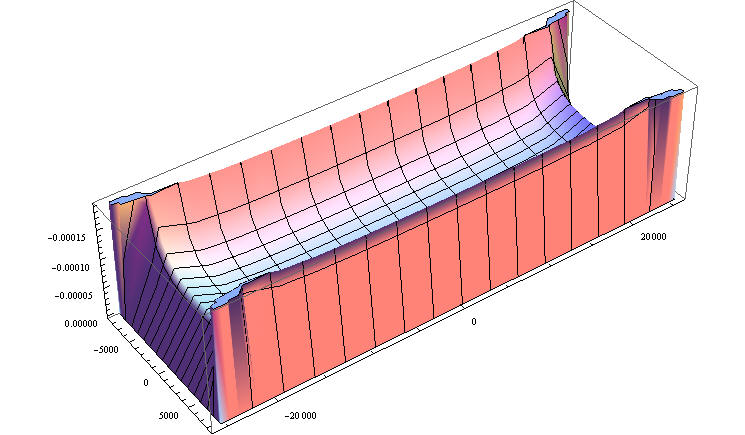
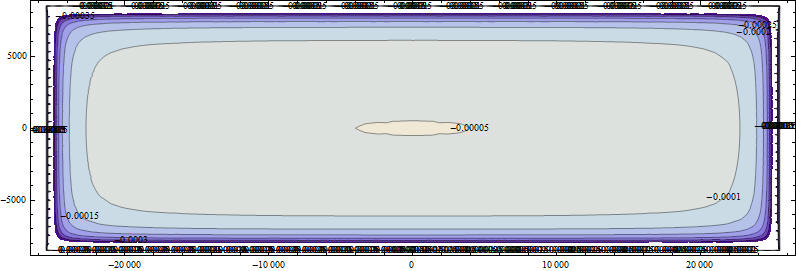
Так как графики строились при единичном перемещении и учитывая соотношение C u=F на них можно смотреть как на распределенную жесткость основания в вертикальном направлении при использовании пружинных моделей грунта типа винклеровского основания если принять, что здание можно рассматривать как жесткое . Сравнив с аналогичным рисунком для постоянного давления на прямоугольник на полупространстве, видно, что жесткость не является независимой от свойств здания хорактеристикой материала полупространства и площадки нагружения и, если ввести некоторым разумным образом понятие гибкости здания, то приемлимую для расчетов жесткость можно определять как некоторую линейную комбинацию из решения задачи Неймана и задачи Дирихле. А коэффициенты линейной комбинации определять по результатам численного моделирования методом конечных элементов.Но по возможности логично все-таки моделировать вместе с землей, а аналитические результаты использовать для краевых условий. на поверхностях разреза конечной области. Необходимо отметить так же неустойчивость определения главного вектора через интегрирование. Из-за фундаментального стремления напряжений к бесконечности на границе, для измерения физических характеристик предпочтительнее опираться на задачу Неймана. Для этого интересно рассмотреть изменение перемещений по глубине и для жесткого штампа, а для давления это было сделано выше.
Ответ на вопрос как согласуются решения Дирихле и Неймана дает рассмотрение главных векторов и соответствующих им перемещений через теорему Бетти из теории упругости, которая гласит - работа системы внешних сил 1 на перемещениях вызываемых системой 2, равна работе системы внешних сил 2 на перемещениях, вызываемых системой 1. В рассматриваемой ситуации симметрии в двух плоскостях главные векторы и наибольшие перемещения им соответствующие в центре площадок нагружения. Таким образом при равенстве главных векторов будут равны и максимальные осадки задач Неймана и Дирихле.
К такому же выводу приводит и рассмотрение работы главного вектора по теореме Клапейрона - упругая энергия равна половине внешних сил на их перемещениях.
Распределение перемещений по поверхности
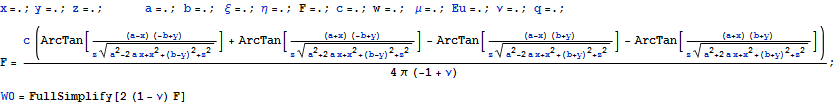
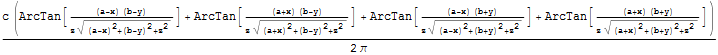
 =>
=> 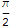
При z=0 получаем с - краевое условие задачи Дирихле, это естественно. Построим график на небольшом удалении от поверхности

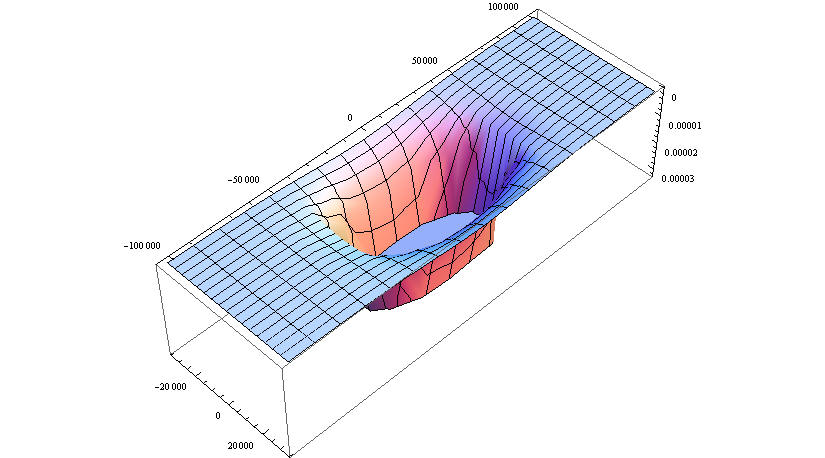
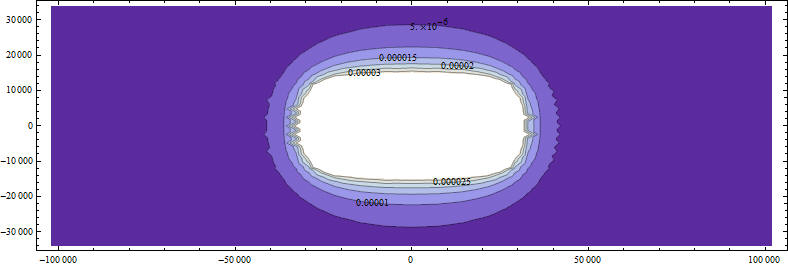
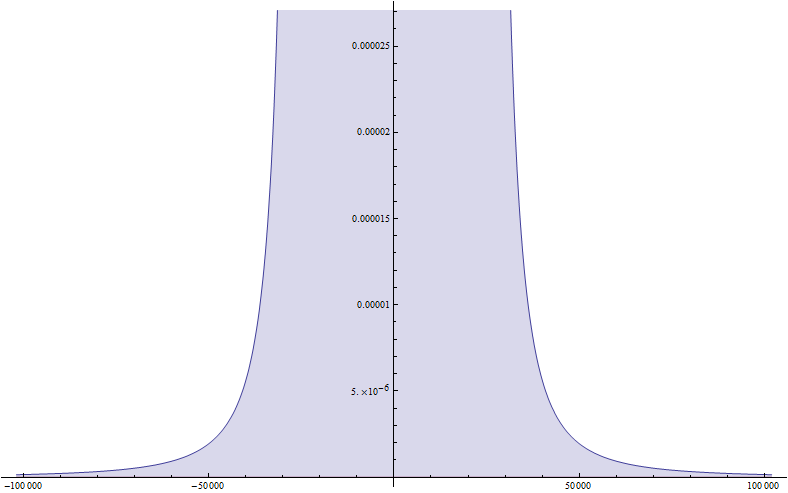
Распределение перемещений по глубине в центре площадки
Ранее приводились соотношение
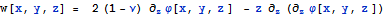 для перемещений, основанное на
представлении Папковича - Нойбера для решения задачи Навье - Коши теории
упругости. Ранее получено выражение для
для перемещений, основанное на
представлении Папковича - Нойбера для решения задачи Навье - Коши теории
упругости. Ранее получено выражение для
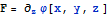 .
Рассматривать будем в начале координат решение задачи Дирихле.
.
Рассматривать будем в начале координат решение задачи Дирихле.

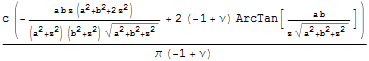
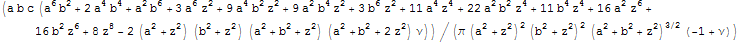
Ранее было получено распределение перемещений по глубине для задачи Неймана при равномерном давлении на прямоугольную площадку полупространства q.
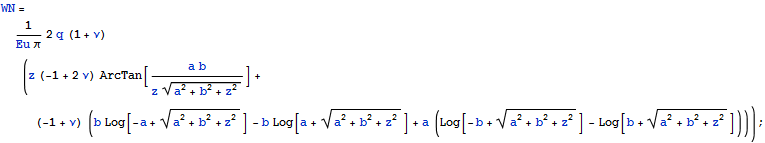
На поверхности перемещение , с учетом ограниченности ArcTan
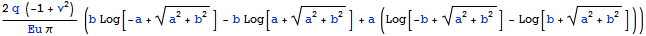
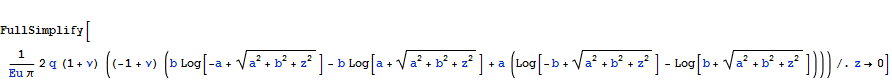
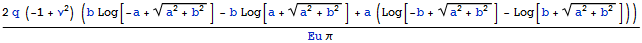
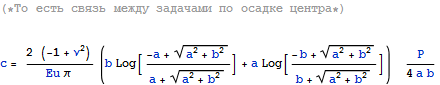
Беря различные жесткие штампы и имея результаты измерений
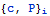 можем построить
переопределенную систему уравнений относительно Eu и Nu. Разрешив ее,
например методом наименьших квадратов, или c помощью другого подходящего
сконструированного функционала можем найти статистически надежные результаты для
осредненного модуля упругости и коэффициента Пуассона. Любопытно промоделировать
такое методом конечных элементов, например. Можно ограничиться и одним штампом,
если привлечь известное из теории упругости соотношение между упругими
константами и скоростью звука в среде, которую можно измерить достаточно надежно.
можем построить
переопределенную систему уравнений относительно Eu и Nu. Разрешив ее,
например методом наименьших квадратов, или c помощью другого подходящего
сконструированного функционала можем найти статистически надежные результаты для
осредненного модуля упругости и коэффициента Пуассона. Любопытно промоделировать
такое методом конечных элементов, например. Можно ограничиться и одним штампом,
если привлечь известное из теории упругости соотношение между упругими
константами и скоростью звука в среде, которую можно измерить достаточно надежно.

44.8202
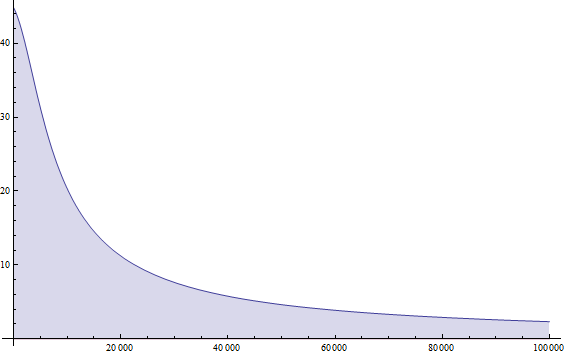
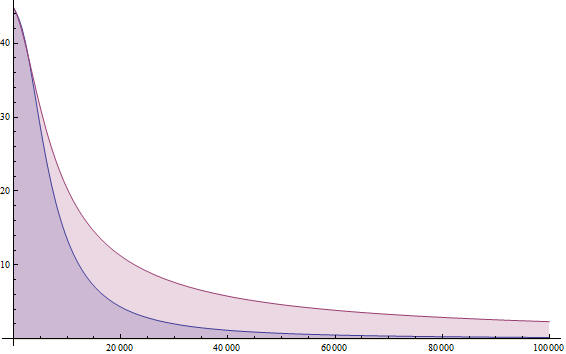
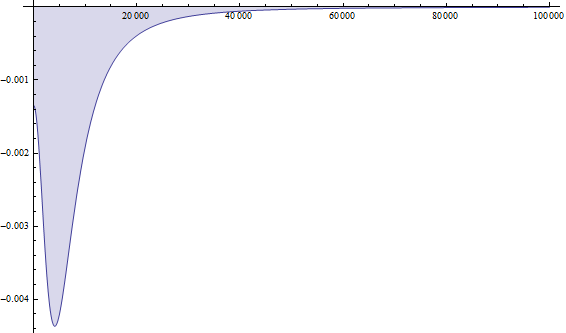
Из предпоследнего графика следует, что затухание осадки в центре происходит быстрее у жесткого штампа. А на последнем показано распределение вертикальных деформаций по глубине. Характер распределения деформаций аналогичен распределению при равномерном давлении
Связь задач Дирихле и Неймана
В общем случае, надо найти напряжения на поверхности некоторого прямоугольного объема полупространства окружающего штамп в задаче Дирихле, проинтегрировать по поверхностям разреза и найти главный вектор. Это позволит точно согласовать задачи, но слишком трудоемко для ноутбука который под рукой автора. Поэтому оценим эту связь более простыми и грубыми методами. В книге Коллинза приведены величины осадок для круглого штампа и для нагружения круга равномерным давлением
 =>
=>
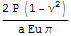
 =>
=>
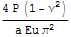
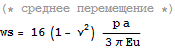 =>
=>
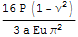
 =>
=>
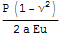
Численно найдем приемлимую комбинацию из величин задачи Неймана для задачи Дирихле.
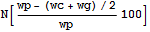 =>
-4.1904
=>
-4.1904
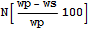 =>
-8.0759
=>
-8.0759
Видим, что с точностью около 4% осадка круглого штампа совпадает с полусуммой максимальной и минимальной осадок для задачи Неймана и эта оценка примерно вдвое лучше чем средняя осадка. Для прямоугольной области нагружения проверим это методом конечных элементов. Для этого воспользуемся следующим кодом на APDL для Ansys:
/clear
/CWD,'d:\tempans' ! рабочий каталог
!*****************************************************************
! прямоугольный штамп в полупространстве
!*****************************************************************
*CREATE,stamp ! __________________
!____________________модель__кГ мм _____________________________
/PREP7
a=10000/2 $ b=5*a $ n=5 $ h=(a+b)*n
! Геометрия
RECTNG,0,a,0,b, $ RECTNG,0,2*b,0,2*b, $ RECTNG,0,n*b,0,n*b,
A,2,6,7,3 $ A,4,3,7,8 $ A,6,10,11,7 $ A,8,7,11,12 $
ADELE,3, , ,1 $ ADELE, 2, , ,1
allsel $ VEXT,all, , ,0,0,a,,,,
ASEL,ALL $ ASEL,S,LOC,Z,a $ VEXT,all, , ,0,0,n*(a+b),,,,
ASEL,ALL $ ASEL,S,LOC,Z,0 $ ASEL,R,LOC,X,0,a $ ASEL,R,LOC,Y,0,b
VEXT,all, , ,0,0,-0.1*(a+b),,,,
NUMMRG,ALL, , , ,LOW
! элементы материалы
m_Gamma = 7.85e-10 ! плотность железа, для железобетона *0.32
Es=21000 ! сталь
ANTYPE,0 $ ET,1,SOLID186
MPTEMP,,,,,,,, $ MPTEMP,1,0 $ MPDATA,EX,1,,1.0 $ MPDATA,PRXY,1,,0.40 !
MPTEMP,,,,,,,, $ MPTEMP,1,0 $ MPDATA,EX,2,,Es $ MPDATA,PRXY,2,,0.40 !
MPTEMP,,,,,,,, $ MPTEMP,1,0 $ MPDATA,EX,3,,0.001 $ MPDATA,PRXY,3,,0.40 !
allsel
TYPE, 1 $ MAT, 1
MSHAPE,0,3D $ MSHKEY,1 $ SMRT,1 $ VMESH,all
! изменение модуля упругости штампа
VSEL,ALL $ VSEL,S,LOC,Z,-(a+b),0 $ ESEL,ALL $ ESLV,S
EMODIF,all,MAT,2, ! 3 - равномерное давление 2 - жесткий штамп
! условия
ASEL,ALL $ ASEL,S,LOC,X,0 $ ASEL,A,LOC,X,n*a $ DA,all,UX,0
ASEL,ALL $ ASEL,S,LOC,Y,0 $ ASEL,A,LOC,Y,n*b $ DA,all,UY,0
ASEL,ALL $ ASEL,S,LOC,Z,n*(a+b)+a $ DA,all,UZ,0
! нагрузка
p=10000/1000000 $ ASEL,ALL $ ASEL,S,LOC,Z,-0.1*(a+b) $ SFA,all,1,PRES,p
allsel
FINISH
!______________________Решение____________________________________
/SOL
/STATUS,SOLU
SOLVE
FINISH
! результат
/POST1
ESEL,ALL $ ESEL,S,MAT,,1 $ PLNSOL, U,Z, 0,1.0
/REPLOT
*END ! конец макроса ______________________________
! ________________________работа_____________________________
*USE,stamp ! подключение макроса ____________
/DELETE,stamp ! удаление макроса ____________
/eof!****************конец файла*************************************
Для стального штампа из стали получаем следующий результат :
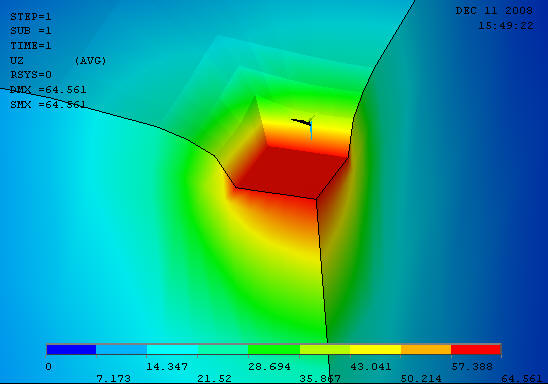
И решение для равномерно распределенной нагрузки :
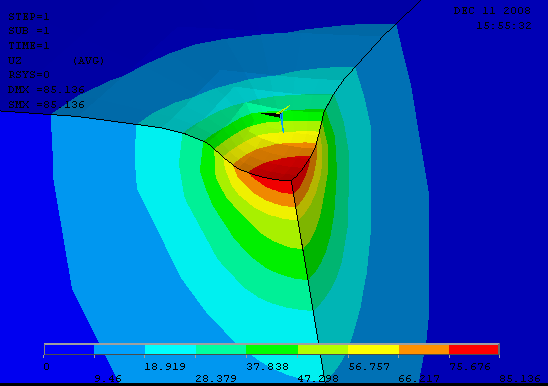
Результаты вертикальных перемещений для центра и угла
NODE UZ
1 85.136
12 43.866
По аналитическому решению для бесконечного полупространства они должны отличаться в два раза. Оценим погрешность в процентах.
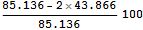 =>-3.0492
=>-3.0492
Оценим погрешность гипотезы о том, что осадка жесткого штампа равна полусумме экстремальных значений для податливого
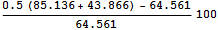 => -0.092935
=> -0.092935
Видим, что погрешность для квадрата значительно меньше одного процента. Ранее было получено решение для равномерно распределенного давления
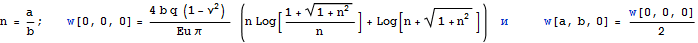
Проверим абсолютные величины
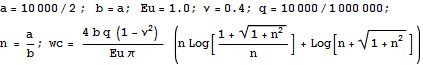 =>
94.264
=>
94.264
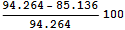 =>
9.6834
=>
9.6834
Видим, что численное решение на 10% более жесткое, чем аналитическое. Это связано с ограниченностью конечной области и малым количеством конечных элементов. Оценим погрешность вносимую ограничением по высоте в численном решении:
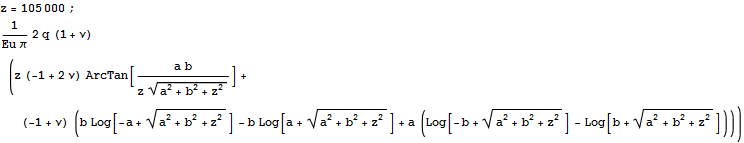 =>
4.6618
=>
4.6618
Вычислим погрешность с учетом корректировки на основе аналитического решения
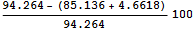 =>
4.7379
=>
4.7379
Проделаем аналогичный анализ для сильно вытянутого прямоугольника
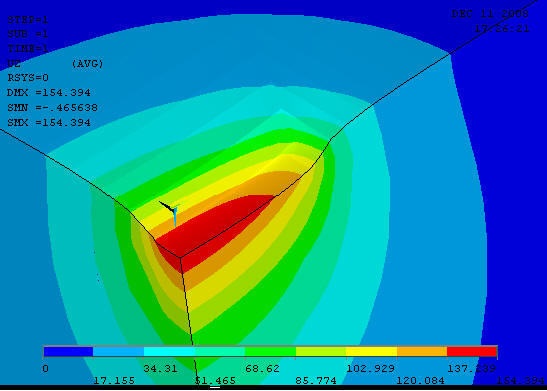
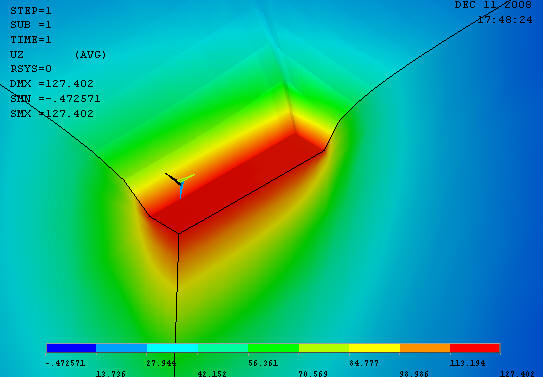
1 154.39
28 82.129
По аналитическому решению для бесконечного полупространства они должны отличаться в два раза. Оценим погрешность в процентах.
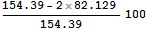 =>
-6.3916
=>
-6.3916
Оценим погрешность гипотезы о том, что осадка жесткого штампа равна полусумме экстремальных значений для податливого
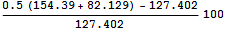 =>
-7.176
=>
-7.176
Из приближенных решений можно сделать вывод, что гипотеза о том, что полусумма экстремальных значений осадок по площадке нагружения является хорошим приближением оценки осадки эквивалентного жесткого штампа.
Такой результат видимо связан с теоремой о среднем для гармонических функций, для которых среднее значение в центре шара равно среднему арифметическому значений на сфере, а в сечении, то есть в одномерном случае для поверхности сфера это два крайних значения, если сферу проводим между максимумом и минимумом осадок. А так как для любого направления кроме угловых осадки эквивалентного жесткого штампа будут больше, то из принципа минимума полной потенциальной энергии надо выбрать наименьшее.
В такой ситуации будет справедлива теорема Бетти и другие энергетические теоремы для главных векторов.
Суперпозиция
Для использования суперпозиции при анализе сложных объектов удобно оформить результаты в виде функции
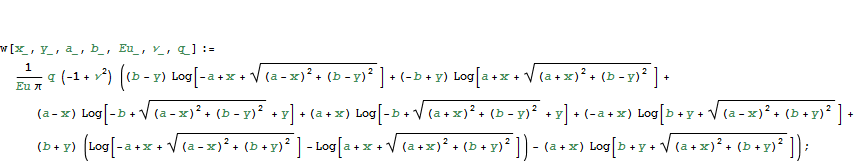

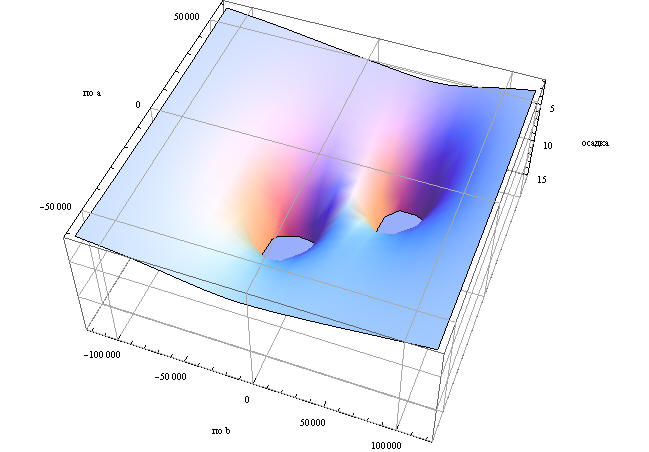
В теории упругости важнейший принцип позволяющий упрощать задачи, сохраняя существо вопроса - принцип Сен - Венана или принцип статической эквивалентности систем нагрузок. Вот как его определяет, например, Хан - "Если тело находится в равновесии под действием двух различных, но статически эквивалентных систем нагрузок, приложенных в малой области, то эти системы нагрузок будут оказывать одинаковое действие на те части тела, которые далеко удалены от места их приложения " C помощью суперпозиций несложно получить оценку концепта "далекой удаленности" , рассматривая воздействие с нулевым главным вектором и моментом по площадке. Для этого рассмотрим квадратную площадку c давлением q и меньшую площадку внутри ее с давлением - q1, которое подберем таким образом, чтобы главный вектор суперпозиции был бы нулевым и для площадок соблюдались условия симметрии.

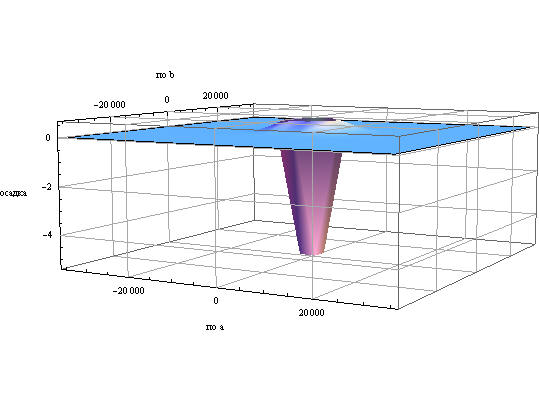
Таким образом всегда можно оценивать понятие "далекой удаленности" для конкретной задачи.
О таком подходе можно посмотреть у Новацкого.
Используя суперпозицию решений при трансформации координат с помощью обычных для машинной графики смещений и поворотов можно оценивать влияние различных объектов прямоугольной формы различных размеров как по отдельности, так и с совокупности. Таким образом можно например получить распределение усилий по сваям в случае жесткого и гибкого фундамента если нагрузку от вышележащих грунтов представить в виде давления по большой площади, а усилия или смещения от свай небольшими областями. Так как основное допущение, позволяющее решение уравнения Навье-Коши к одной гармонической функции касается отсутствия касательных напряжений на поверхности полупространства, как указано у Работнова то не просматривается никаких принципиальных ограничений, чтобы не сместить область нагружения по которой осуществляется интегрирование внутрь полупространства, а это позволит решать и задачи для свайных полей и без замены верхних слоев распределенной нагрузкой. Для проверки через предельные переходы существует задача Миндлина о сосредоточенной силе внутри полупространства. Кроме того видимо возможно и разместить область нагружения вертикально, или под углом. Но тут надо пробовать и думать куда приспособить такие решения :) Возможно к расчету шпунтовых ограждений и стен в грунте. Эти задачи еще ждут своих постмодернистов :)))
Напряжения, горизонтальная нагрузка и другие механические результаты
Как писалось выше, из решения Папковича-Нейбера для однородного уравнения Навье-Коши для полупространства получается функциональное представление для перемещений через гармоническую функцию
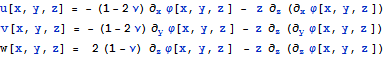
Для вертикальных перемещений хватило производной по z от
гармонической функции  - F. Для определения
перемещений по другим направлениям надо найти
- F. Для определения
перемещений по другим направлениям надо найти 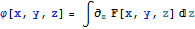
и далее найти функции перемещений, затем используя
соотношения Коши найти деформации и, используя закон Гука, найти напряжения.
Покажем, что интегрирование для отыскания
 несложно осуществить например для задачи Неймана
несложно осуществить например для задачи Неймана

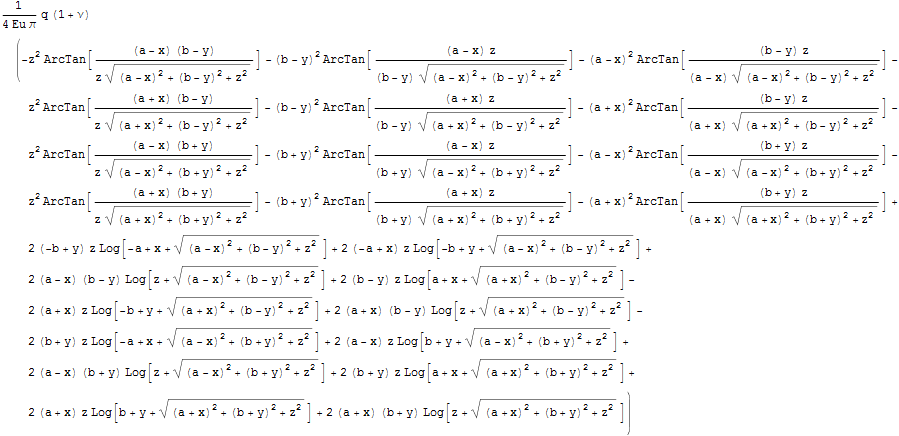
Дальнейшие упражнения в математическом постмодернизме автору пришлось оставить из-за слабости мозгов у ноутбука. Надеюсь заинтересованные читатели смогут осуществить без особого труда сами :) Это может оказаться полезным в эволюционных задачах, связанных, например, с ползучестью грунтов. И, учитывая, что решение нелинейных задач технологически связано с последовательностью линейных, то и задач пластичности.
Полезно помнить о том, что все достаточно гладкие решения эллиптических уравнений, а уравнения теории упругости и являются такими хоть в перемещениях, хоть в напряжениях, с аналитическими коэффициентами являются так же аналитическими функциями. Эта гипотеза была высказана Гильбертом в 19 его проблеме и доказана Бернштейном, как отмечается в книге Михлина.
Заключение
Используя представленную технологию можно получить аналитические решения и для объектов в других системах координат, например цилиндрических и элиптических для этого достаточно сделать соответствующие замены переменных и осуществить интегрирование не всегда правда это легко сделать. Судя по литературе иногда удается проинтегрировать фигуры типа треугольников, полуокружностей, что в общем полезно для более гибкого использования суперпозиции решений. Есть еще вопрос сведения неоднородных сред к однородным, но эти вопросы достаточно подробно освещались в предыдущих статьях. На основе представленных соотношений меняя формы штампов несложно организовать и испытания для получения переопределенных нелинейных систем уравнений относительно модуля Юнга и коэффициента Пуассона, разрешая которые, например с использованием наименьших квадратов, или конструируя другой функционал, можно получить более статистически достоверную информацию о сразу осредненных механических характеристиках грунтов. В любом случае аналитические решения полезны, так как позволяют более обоснованно выбирать области моделирования бесконечного полупространства конечными элементами, ставить корректные краевые условия, что несложно сделать например через макросы в профессиональных программах типа Ansys. Оценивать хотя бы порядок цифр полученных численных решений. Кроме того, позволяют оценить влияние на окружающую застройку в требуемых нормами объемах. Хотелось еще описать вопросы армирования железобетонных элементов, сравнение с подходом Eurocode, но уж в другой раз :)
Литература
Курс математической физики, Михлин С.Г., Наука, М.1968
Механика деформируемого твердого тела Работнов Ю.Н. , Наука,М. 1988
Механика контактного взаимодействия ,Джонсон К. , Мир, М.1989
Теория упругости, Хан Х, Мир,М 1988
Теория упругости, Новацкий В. Мир, М.1975
Love A.E.H.,The stress produced in a semi-infinite solid by pressure in part of the boundary,Phil.Trans.Royal Soc.,1928-1929,N 228,377-420.
Механика грунтов, Тер-Мартиросян З.Г. М.2005
Методы и средства определения полей деформаций и напряжений, Пригоровский Н.И. Машиностроение, М. 1983
Геотехническое сопровождение реконструкции городов, В.М. Улицкий, А.Г. Шашкин М.1999
ноябрь-декабрь 2008